
Logic gates
by Chris Woodford. Last updated: May 18, 2023.
You probably know that calculators and computers store decimal (0–9) numbers as long strings of zeros and ones in a form called binary code. Each number is stored using microscopic electronic switches called transistors. It's easy to store binary numbers simply by switching transistors on and off. Switching on a transistor stores a number one; switching it off stores a zero. So storing numbers is easy. But how can you add, subtract, multiply, and divide using nothing but electric currents? Calculators and computers do this using clever electronic circuits called logic gates. Let's take a closer look at what they are and how they work.
Photo: A gate can keep you out or let you into a field. In the same way, a microscopic logic gate is a barrier in an electronic circuit that can let electricity through or stop it flowing altogether. Put lots of logic gates together and you make a machine that's capable of basic mathematical "reasoning."
Sponsored links
Contents
What are logic gates? Circuits that compare!
A logic gate might sound horribly complex, but it's simply an electric circuit with two inputs and an output. It receives two incoming electric currents, compares them, and sends on a new, outgoing electric current depending on what it finds. A logic gate is a bit like a doorman or bouncer who is allowed to let people into a nightclub only if they pass certain tests. There are quite a few different types of logic gate, the most common of which are called AND, OR, NOT, XOR (Exclusive Or), NAND (NOT AND), and NOR (NOT OR). Let's look at the three simpler ones, AND, OR, and NOT:
AND
Suppose you go to a nightclub where the doorman's job is to enforce a simple rule: "Everyone in your group must wear a tie to come in". You go along with a friend one night. If you're both wearing ties, you'll get in. If only one of you is wearing a tie, or if neither of you is, neither of you will get in. An AND logic gate works the same way with two electrical inputs. If both inputs are switched on (that is, carry a number 1), the output will be 1 as well. Otherwise the output will be 0. In electronics, we can represent an AND gate with this little symbol. Three ways in which the gate can work are shown below.

OR
You're not wearing a tie, so you go to another club further down the street. Here, the person on the door is enforcing a different rule: "A group of people can come in if any one of them is a member". If either you or your friend is a member, or if you both are members, you can both come in. If neither of you is a member, you're both left out in the cold. An OR logic gate works this way with two electrical inputs. If either input is switched on (that is, carries a number 1), the output will be 1 as well. Otherwise the output will be 0. In electronics, we represent an OR gate with a different symbol. Three ways in which it can work are shown beneath:

NOT
So far, you've failed to get into either of the clubs. But there's one last hope: you know a friend is having a party a few streets away. The only trouble is, there's a really argumentative and contrary person on the door. He talks to each person in turn as they approach him. If you're nice and polite, he shouts abuse at you and turns you away. But if you're rude to him, he likes that for some reason and lets you in. In other words, he does exactly the opposite of what you'd expect! In electronics, there's a logic gate that works in the same, contrary way and it's called a NOT gate or inverter. Unlike AND and OR gates, it has only one input and one output. The output is exactly the opposite of the input, so if the input is a 0, the output is a 1 and vice versa. Here's how we represent a NOT in electronics. Two ways it can work are shown beneath.

The other three common logic gates are variations on these three. XOR (Exclusive OR) is like an OR, but it switches off if both the inputs are switched on. NAND is just like AND, only the end result is swapped over (so where AND produces an output of 1, NAND produces an output of 0). NOR is like OR with the end result swapped over in the same way.
Summarizing logic gates with truth tables
Computer chips don't really work like nightclub doormen: they just turn inputs into output—ones into zeros and zeros into ones. We can summarize how they work very quickly and simply by writing what's called a truth table. This shows the output you get (one or zero) for every possible input (each separate row of the table describes one of the possible sets of inputs and output). Here are the truth tables for the logic gates we met up above:
AND (Output only with all inputs)
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
OR (Any input produces an output)
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
NOT (Inverter)
| Input | Output |
|---|---|
| 0 | 1 |
| 1 | 0 |
XOR (Exclusive OR)
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NAND (AND with outputs reversed)
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Controlling a calculator display with logic gates
Calculators can do all the things they need to do using different combinations of logic gates. It's logic gates that control how the display works in a calculator and more logic gates that figure out the results of calculations.
For example, each segment of a calculator's display is switched on and off by a series of logic gates that are connected together. Consider just the bottom lower right segment (shown in the picture, right, in blue). We need to turn this segment on if we're showing the numbers 0 (binary 00), 1 (01), 3 (11), 4 (100), 5 (101), 6 (110), 7 (111), 8 (1000), and 9 (1001)—but not if we're showing the number 2 (10). We can make the segment switch on and off correctly for the numbers 1–10 by rigging up three OR gates and one NOT gate like this.

If we feed the patterns of binary numbers into the four inputs on the left, the segment will turn on and off correctly for each one. For example, feed in the number 7 as the four inputs 0111 and the gates will trigger like this, correctly switching on the segment:
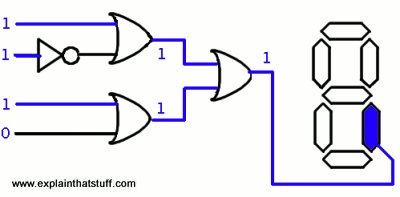
The other six segments of each digit are controlled by other combinations of logic gates.
Calculating with logic gates
It's possible to do any calculation you can think of by combining a different pattern of logic gates. The gates compare and combine two series of binary numbers, corresponding to the decimal numbers in your calculation, and produce a new series of binary numbers equal to the result. Addition is carried out by circuits called half-adders and full adders (which can carry on the results of a previous addition); subtractors work in a very similar way; multipliers use a collection of AND gates to multiply two numbers with a series of additions You can find more details about this in our article on calculators.
Test your knowledge of logic gates
A good way to test your grasp of logic gates is to download one of the many apps that teach you about them. Most of them are quite similar. After running through the basics of how the different gates work, they present you with increasingly complex circuit patterns and invite you either to work out what the final output will be or which gates to use to achieve a certain output with a certain input. If you're new to circuit logic, I'd recommend trying one or two just to make sure you've grasped the concepts; search for "logic gates" in your favorite app store.

Screenshot: Above) Circuit Scramble by Suborbital is an educational Android app that teaches you the basics of logic gates. In this very simple example, you have to figure out which of four inputs (bottom) to activate so that two OR gates and an AND gate produce an output at the top. Below) Logic Gates by Cyfrogen is a similar Android app. This time you're given the inputs (left), the output (right), and one of the gates, and you have to choose which other gate to use in the blank space (NAND or AND) to make the circuit work.

Who invented the idea?
“Boole was one of the most eminent of those who perceived that the symbols of operation could be separated from those of quantity and treated as distinct objects of calculation.”
Popular Science, October 1880.
This logical way of comparing numbers to make decisions that produce either a yes or no, 1 or 0, true or false is called Boolean algebra after its discoverer, English mathematician George Boole (1815–1864), who set out the idea in an 1854 book titled An Investigation of the Laws of Thought, on Which Are Founded the Mathematical Theories of Logic and Probabilities. His objective was to show how complex human reasoning could be represented in a logical, mathematical form.

Photo: George Boole, in an illustration from Popular Science Magazine, 1880 (with colors added).
Popular Science magazine paid tribute to him in its October 1880 issue with these words:
“George Boole was a man of a very high order of genius, a profound and most original thinker of this century, who will be known in future by his contributions to mathematical and logical science. Yet he can never be widely known, for his work was so recondite that those who can properly appreciate it will always be but very few.... An Investigation of the Laws of Thought... is Boole's greatest work, and is an attempt to apply the symbols and operations of mathematics to logic and the laws of thinking.”
